Addition Properties of Inverse Trigonometric Functions - Cuemath: Addition Properties Of Inverse Trigonometric Functions in Trigonometry with concepts, examples and solutions. FREE Cuemath material for JEE,CBSE, ICSE for excellent results!. The sum and difference of inverse trigonometric functions ... - MATHVOX: The difference of arcsines. Proof of the formula for the sum and difference of arcsines. Step 1. To prove the formula for the sum of arcsines, let’s introduce new notations: and: According to the new notations: For any values of x and y, arcsin d will belong to the interval [−π/2; π/2].

CBSE Inverse Trigonometric Functions Class 12 Mind Map For Chapter 2 Of ...

Step 2.. Inverse trigonometric functions - Wikipedia: The following table shows how inverse trigonometric functions may be used to solve equalities involving the six standard trigonometric functions. It is assumed that the given values θ , {\displaystyle \theta ,} r , {\displaystyle r,} s , {\displaystyle s,} x , {\displaystyle x,} and y {\displaystyle y} all lie within appropriate ranges so that the relevant expressions below are well-defined .. Inverse Trigonometric Identities | Brilliant Math & Science Wiki: The following inverse trigonometric identities give an angle in different ratios.

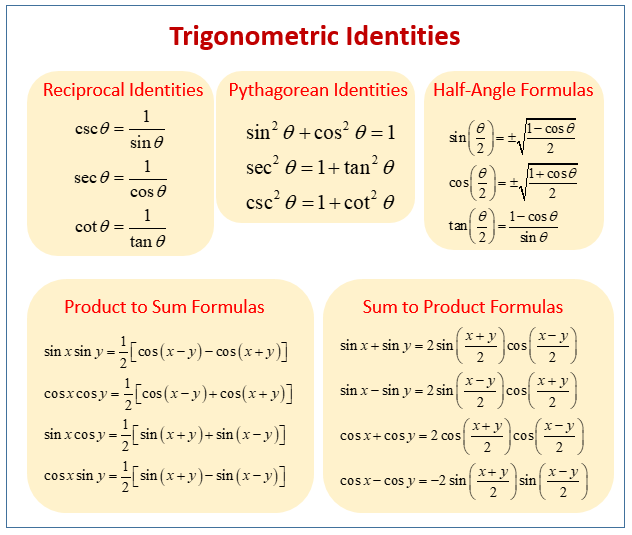
Trigonometric Functions (examples, Videos, Worksheets, Solutions ...

Before the more complicated identities come some seemingly obvious ones. Be observant of the conditions the identities call for. Now for the more complicated identities. These come handy very often, and can easily be derived using the basic trigonometric identities.. 6.3: Inverse Trigonometric Functions - Mathematics LibreTexts: In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in Figure 6.3.1. Figure 6.3.1. For example, if f(x) = sin x, then we would write f − 1(x) = sin − 1x.

Inverse Trigonometric Values

Be aware that sin − 1x does not mean 1 sin x. The following examples illustrate the inverse trigonometric functions:. Identities with Inverse Trig Functions - University of California, Berkeley: Summary. Review: \Inverse" trig functions. Identies: Compositions of sin( ) and sin. 1(y). Example: Inverting functions with terms from trig Trig Identities: Right angle Identities Trig Identities: Even and Oddness.. Inverse Trigonometric Functions - Formulas, Graph, Domain & Range - Cuemath: Inverse trigonometric functions are the inverse functions of the basic trigonometric functions which are sine, cosine, tangent, cotangent, secant, and cosecant functions.

How To Calculate Inverse Trig

Some basic inverse trigonometric formulas are as given below, sin -1 (-x) = -sin -1 x. tan -1 (-x) = -tan -1 x. cosec -1 (-x) = -cosec -1 x.. 8.2 Inverse Trigonometric Functions – Trigonometry: The inverse sine function. The function f(x) = sin − 1x is defined as follows: sin − 1x = θ ifandonlyif sinθ = x and − π 2 ≤ θ ≤ π 2. In other words, sin − 1x is the angle in radians, between − π 2 and π 2, whose sine is x. There are many angles with a given sine value x, but only one of these angles can be sin − 1x..

Trigonometry Formulas With Examples